Rollout and Agentic RL (Legacy)#
Note: While this legacy approach works, we strongly recommend using AReaL-lite for new projects. It provides better flexibility, cleaner abstractions, and easier maintenance.
Step 1: Define Your Agent Class#
Create a new file under realhf/impl/agent/, such as math_multi_turn_agent.py. Your
Agent must implement the interface defined in realhf/api/core/agent.py, which
requires a single method: collect_trajectory.
class MathMultiTurnAgent(Agent):
async def collect_trajectory(
self,
prompt: SequenceSample,
env: EnvironmentService,
obs_queue: asyncio.Queue,
act_queue: asyncio.Queue,
):
# Implementation goes here
...
Step 2: Implement the Trajectory Collection Logic#
The collect_trajectory method takes a task prompt, an environment, and two
communication queues. Within this method, you control the data flow between your agent
and the inference engine using these queues:
obs_queue: Send observations (token IDs and generation config) to the inference engine
act_queue: Receive actions (generated responses) from the inference engine
Here’s how the multi-turn conversation works:
for turn in range(self.num_turns):
# Send the current state to the inference engine
await obs_queue.put((qid, token_ids, self.gconfig))
# Get the generated response
act: BundledGenerationOutputs = await act_queue.get()
# Evaluate the response through the environment
success, rewards = await env.step((qid, answers))
# ... process results ...
Environment Integration#
The environment follows a
Gym-like interface with reset and
step methods, but uses asynchronous implementations to prevent blocking across
different environment instances.
For math problems, the environment is typically stateless and acts as a wrapper around your reward function:
class MathCodeSingleStepEnv(EnvironmentService):
async def step(self, action: Tuple[str, List[str]]):
qid, answers = action
# ... setup code ...
# Run reward computation asynchronously
format_rewards = await asyncio.to_thread(
math_verify_call,
answers,
# ... other parameters ...
)
return None, format_rewards, True, False, {}
Handling Multi-Turn Feedback#
After receiving the reward from env.step, check if the answer is correct. If not,
provide feedback and continue to the next turn:
for turn in range(self.num_turns):
# ... generation and evaluation code ...
# Provide feedback based on the result
if success[0]:
feedback = "Congratulations! You are correct!"
else:
feedback = "Unfortunately your answer is wrong. Let's try again."
# Format feedback as a user message
feedback = "\n" + self.tokenizer.apply_chat_template(
[{"content": feedback, "role": "user"}],
add_generation_prompt=True,
tokenize=False,
)
# Add feedback tokens to the conversation
feedback_tokens = self.tokenizer(feedback)["input_ids"]
token_ids.extend(feedback_tokens)
Step 3: Register and Configure Your Agent#
First, register your agent implementation:
# in realhf/impl/agent/math_multi_turn_agent.py
register_agent("math-multi-turn", MathMultiTurnAgent)
# in realhf/impl/agent/__init__.py
import realhf.impl.agent.math_multi_turn_agent
Then update your experiment configuration in
realhf/experiments/async_exp/async_math_ppo.py:
@dataclasses.dataclass
class AsyncPPOMATHConfig(AsyncRLExperimentConfig, PPOMATHConfig):
# Add any new CLI arguments your agent needs
my_param: float = 1.0
@property
def agent(self) -> AgentAbstraction:
return AgentAbstraction(
"math-multi-turn", # Your registered agent name
args=dict(
# Pass any arguments needed for your __init__ method
my_param=self.my_param,
# ... other configuration ...
),
)
@property
def env(self) -> EnvServiceAbstraction:
# Update to use your custom environment if needed
return EnvServiceAbstraction(
"math-code-single-step",
args=dict(dataset_path=self.dataset.path)
)
Step 4: Run Training#
Follow the standard training procedure outlined in the quickstart guide. Launch your experiment with:
python3 realhf/training/main_async_ppo.py my_param=5.0 # plus any additional CLI arguments
Training Results#
Here’s an example of the training reward curve from our multi-turn math agent:
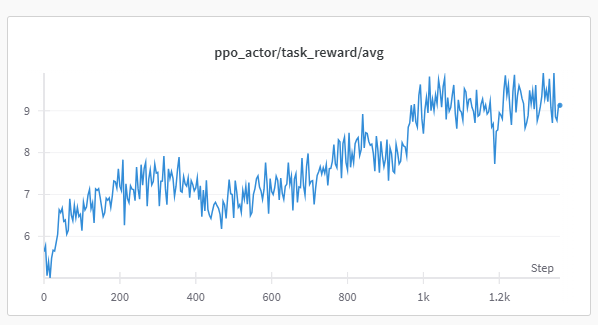
The agent successfully learns to solve math problems with improved accuracy over time, demonstrating the effectiveness of the multi-turn approach.
